Slice

Cheesy? Maybe. Probably. Very. But the iconic trope of waving a sharp around an enemy and... for a split second, nothing happening! Then, the various segmented parts of the body start sliding along perfect planes onto the floor... it's timeless. Reality has a sad shortage of frictionless atom-thick blades, but hey I choose to install the physics engine if I want to!

I did. This one. But I left out all the limiting parts nobody needs in a satisfying slicing demo, so you can demolish your favorite shape to your heart's content.

Why cutting a 2D polygon is kind of a giant pain

For this problem, we have a set of arbitrary simple polygons (define simple: polygons do not intersect themselves but may be non-convex) and mouse pointer coordinates. Both this set's positions and mouse positions are sampled in discrete time, so the mouse historical path is a polyline.

About the definition of shapes in memory: polygons and polylines are arrays of coordinates and have an order that induces an implicit direction. This ordering also gives rise to a natural representation of points by the number of points away from the start, plus the fraction between the surrounding waypoints. Getting the direction of the line at that point, finding features nearby on the line, and splitting the line are all easy with this representation. I've been calling it an "arclength parameter" (plagiarizing from line integrals) and hopefully it's not too obnoxious that I continue to call it so...

The core of the algorithm is just two steps, to differentiate two classes of interactions between the mouse and polygons.

1. Most of the time, the mouse will enter a polygon, spend some time moving inside, and leave. We can take this path it draws during this time and partition the parent polygon with it.

   

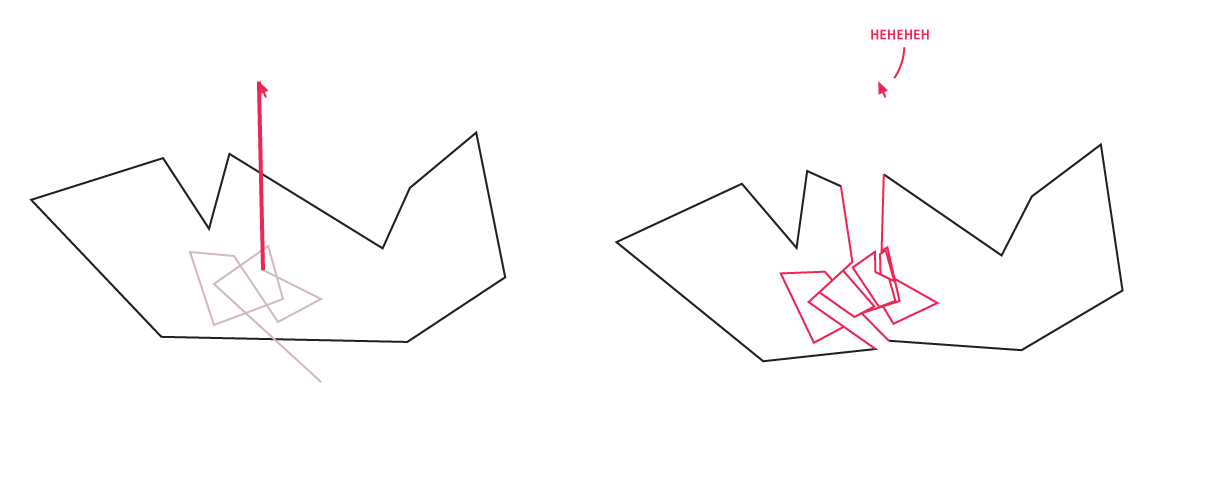
2. Occasionally, the mouse will enter and leave one or many polygons all in one timestep, in a kind of awesome swipe of carnage.

   

   • This is a bit weirder than 1. because we have to be careful about dividing the descendants correctly when they rearrange the order of the coordinates of the parent. We avoid all that noise by just spawning all the daughters before deleting the parent. This bulk approach is effectively what separates this scenario from 1.

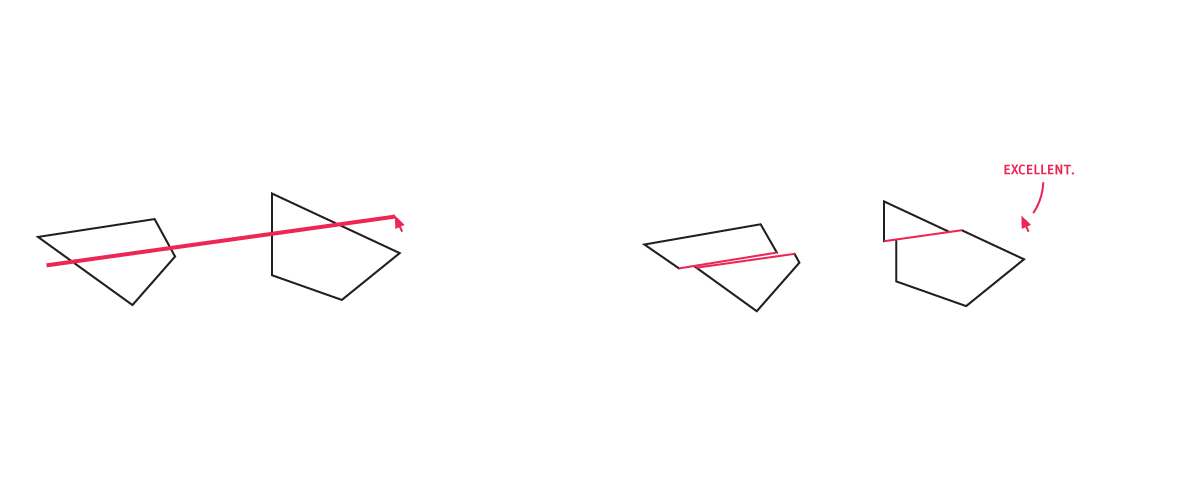
To clarify this is not a dichotomy, 1) and 2) can happen simultaneously, and of course this leads to more fun! Notably, if we cut the polygon according to 1) first then we look at line intersects, the line will come very close to cutting the two daughter polygons again where the mouse cursor first exits.

The solution to this in slice high-level is to ignore edges near the exit point of the mouse cursor, which can be straightforward with some care. In particular, the points in the daughter polygon are oriented so that the first and second points are the edge along which the mouse exited. Then just disabling this edge and the two adjacent ones suffices to fix this.

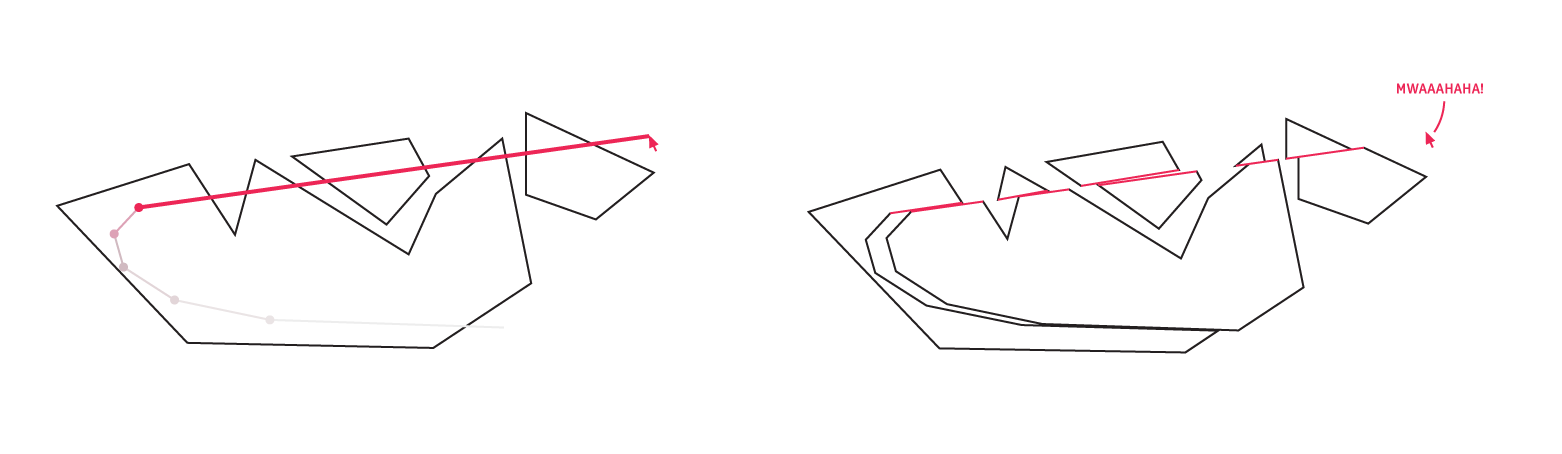
Subproblem: Finding the exterior and interior of a self-intersecting polyline

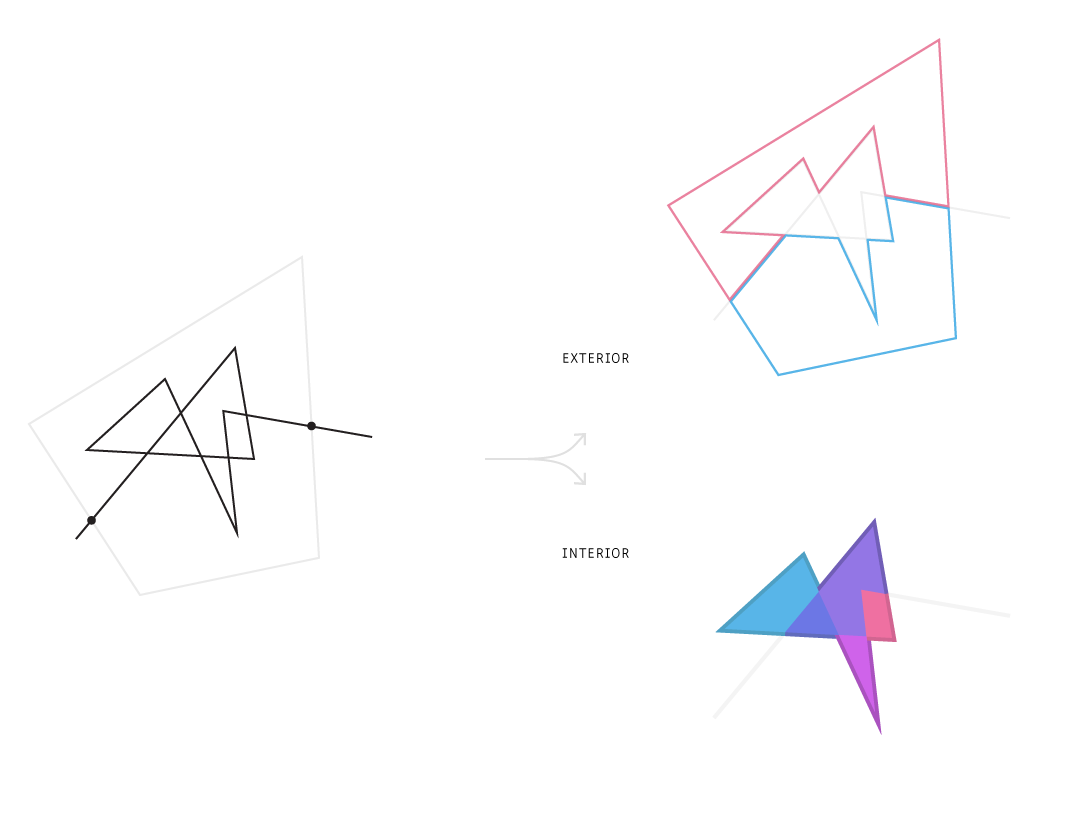
Consider that the path that the mouse can carve inside a polygon can intersect itself, and in real life this would carve out a fresh shape wherever the self-intersections encircle an area.

Finding internal edges by their own merit is pretty expensive, since it's reduceable to point-in-polygon. First then, let's try to find external edges by setting off from one endpoint and turning as sharply as possible at every intersection, left or right every time.

Much simpler and faster. It assumes you start and end outside of the glut of intersections and polygons in the middle. (Do note and be abhored by the very marginally possible corner case where the internal path kisses the boundary of the polygon right at the entry point.)

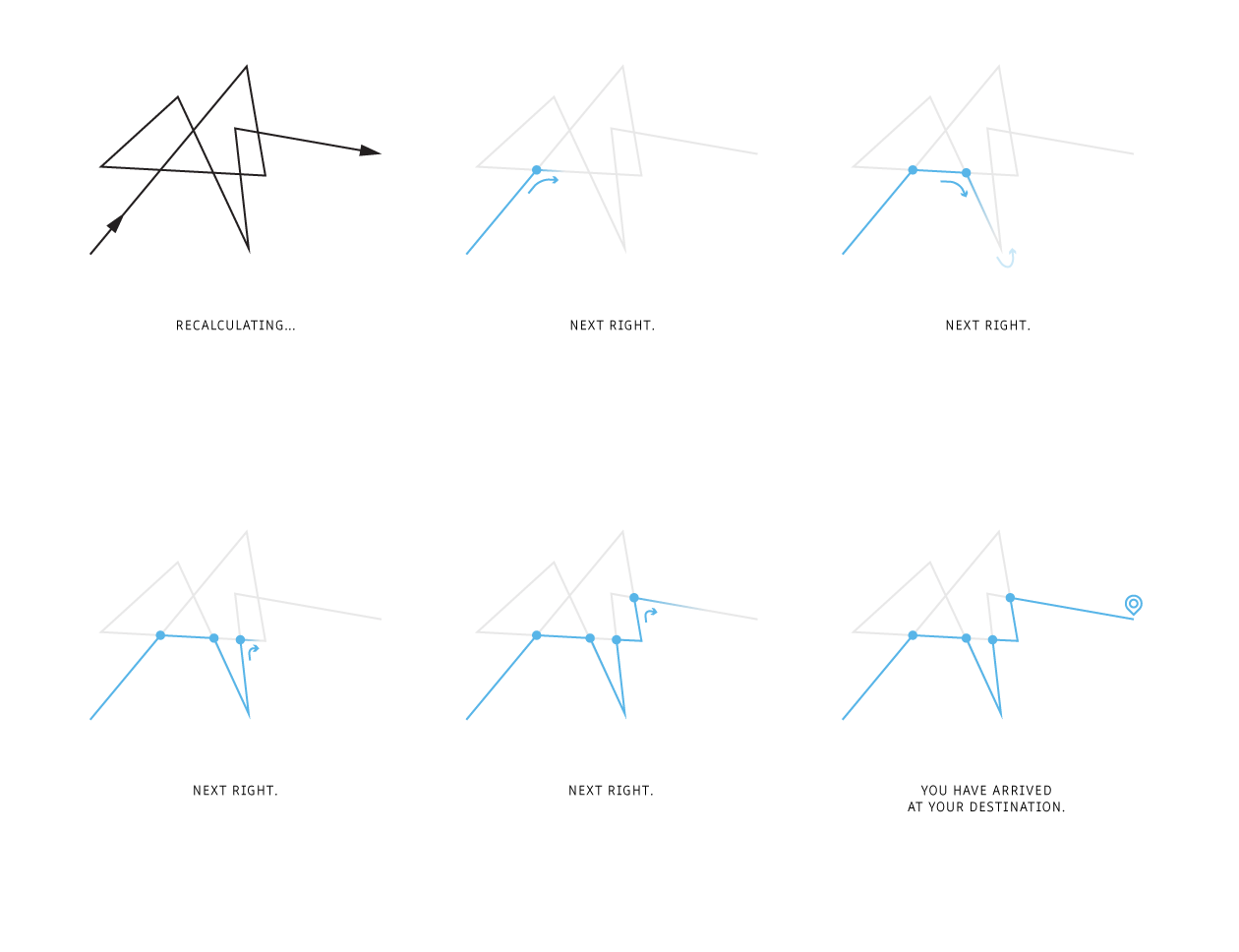
After subtracting the external edges out of the edge set, the remaining edges are all internal! Extracting the interior polygons reuses find_exterior actually, under which the base case is completing a cycle, as opposed to reaching an endpoint of the path. The rest is just maintaining a visited list comprising of the edge and a normalized direction that's been travelled (CW vs. CCW relative to the decreasing arclength parameter).

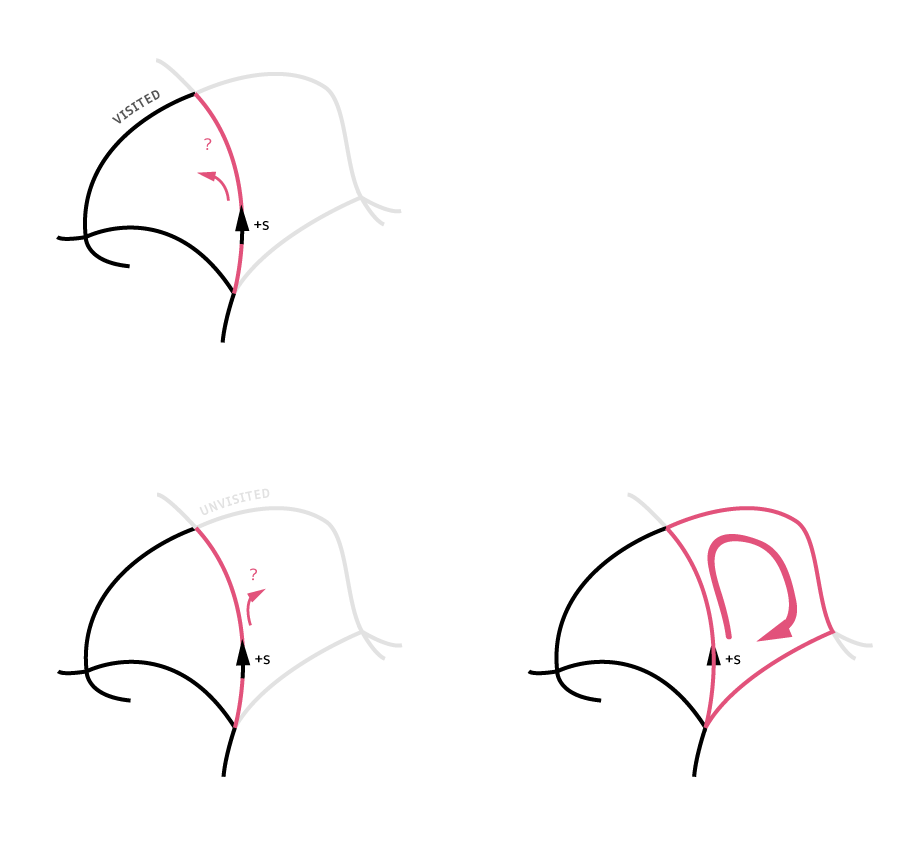
Subproblem: Knowing when something's been cut

I underestimated a lot of problems during the year this project was in on-and-off development. But one underestimation absolutely trumps them all. How do you know whether the mouse cursor is currently in a polygon? As time progresses, the cuts produce more and more edges, so point-in-polygon methods seem prohibitively expensive. Instead, it seems nicer to track when the mouse pointer crosses over an edge in a polygon, since if it happens an odd number of times, the mouse has either exited or entered. However, I had to battle a surprising number of difficulties with this:

1. Since the polygons are all moving, each one actually needs to keep track of the mouse in its own reference frame of position and orientation. This is the case anyways while polygon is in the process of being cut (see gif below) but now it needs to happen all the time.

   

2. The line intersection algorithm has to be opinionated about at least one thing: whether the endpoints are included. In my case, I opted for a "semi-open" rule, where if one of the endpoints of one line segment lies on the other, then whether it's an intersection or not depends on which point it is. That way intersections aren't double-counted or missed when that happens as with a fully closed or open rule respectively. However, the next line segment doesn't carry enough information about whether it's heading further in or actually exiting again! Check out the worst case:

   

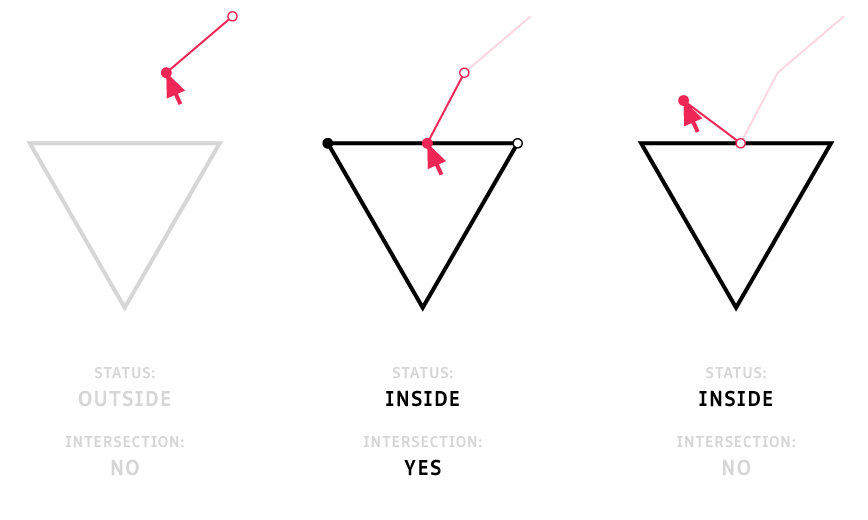
   To compensate for this requires a bit of extra mess. I tack a point-in-polygon check following an intersection, which I could keep doing if the results are inconclusive (e.g. if the mouse continues to trace the boundary of the polygon like an idiot). Remembering the direction of the line segment from the intersection event is another option for example.

3. In a similar vein, if the mouse overlaps its own path within a polygon along a line segment instead of at a point, the boundary-searching algorithm could take one wrong turn and just like that, enter an infinite loop. The discrete pixel coordinates of the mouse pointer makes exact intersections like this substantially more likely, so to ease the pains of numerical instability, I bit the bullet and nudged all the mouse coordinates by a random $\epsilon$ offset.

In the end, point-in-polygon might not be substantially more expensive when combined with a rectangular bound check. Don't get me wrong. I pity my CPU (GPU one day! #goals) to have to run this. I think this is testament to how surprisingly difficult it is to keep this demo interactive (60fps) even when the mouse is totally stationary and outside of all polygons.

Argh, it's still not perfect.

You can play around with the engine above and leaf through it on Github. There are still corner cases abounds, which I'm fairly certain comes from numerical instability at this point. It doesn't help that Matter.JS has its own gripes with some of the geometry and will just totally refuse to bonify some polygons as simulated bodies if they're nasty enough.

So, parting thought. If anyone reading this knows how in the hell Adobe's Pathfinder divide works, please please please break an NDA or two and tell me 🙂