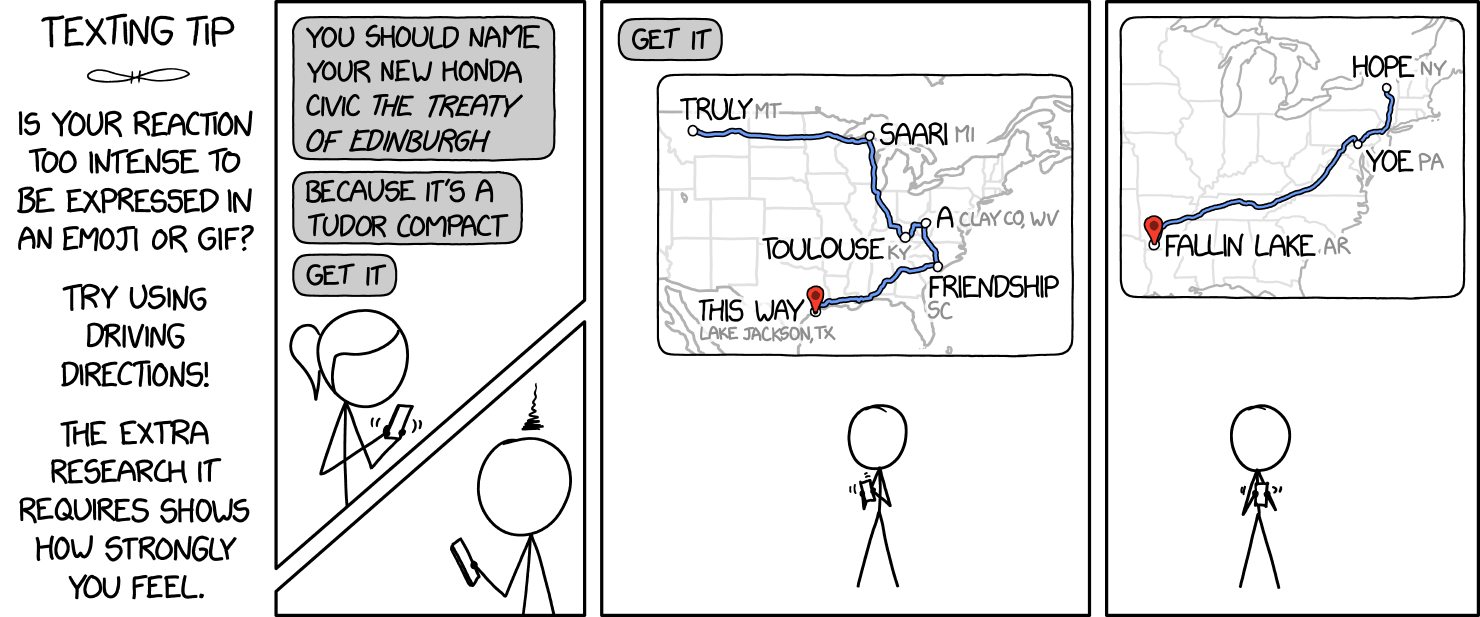
XKCD's Reaction Maps with n-gram matching

I got a good laugh out of this recent XKCD strip, partly because I love puns, and partly because it's pretty hypocritical for Cueball to express his disdain for a one with 9 more:

^{© Randall Monroe, 2020}

Then it started to get me thinking. Getting a solid string of homophonous place names has to be pretty hard to do manually. Could a computer do it better? I should mention Randall has cautioned on the danger of thinking about problems. Or maybe the fun of making other people think about them. And sure enough, I was picked off cleanly.

The long and short is that I cancelled all my appointments for the week (all 0 of them) and made a phrase-to-map-directions converter at maps.lam.io.

I strongly suggest saying the result out loud a few times without gaps between words to see the effect, and your mind will click onto the meter needed to approach your phrase.

Depending on your standards jokes and their byproducts, you may see the where the results seem to try, but fall short of the mark a decent proportion of the time. Well, while I see this as merely a "suggester" of your next road trip to the doghouse, I really think part of the problem may legitimately be that it's hard to find homophones from places.

Ultimately, I'm satisfied with the quality-speed tradeoff of the first prototype. I think generally, place names might not make very good words. And that's maybe why we named them that way.

So all that aside, how does this work?

General approach

At its core, the problem is really this: find an efficient way of sampling the power set of place names $\mathcal{P}(L)$ that will fit in the target phrase of length $N$, i.e. $\{l \in \mathcal{P}(L) | \sum{ len(l_i) } \le N \}$. The solution space is way too big for brute force of course. With millions of place names, and phrase length to place name ratios of 5 or more, there are easily trillions of trillions of combinations.

Not to mention that there is an immediate win to this generally, just by dynamic programming: we step through the phrase and right-align the candidate term, and use the best result up to where the start of the candidate term would land. In other words, over the set of places L, the target string t of length N, and the scoring function for two substrings $s(\cdot, \cdot)$:

$$C[n] = max_{l\in L} \left\{ s(p,t[n-len(l):n]) + C[n-len(l)] \right\}$$

This reduces our effort to $\mathcal{O}(|L|N)$ which is better, but is still in the order of tens (N) of millions (|L|) of queries.

I believe this is as far as an exact solution can get. As far as I've reasoned, impossible to be greedy and exact, because this necessitates an order of processing the string (e.g. making a decision of the subset to narrow to from a set of characters) whereas an exact solution must consider the string entirely at once. In other words, you can always be cutting out the optimal solution except in very narrow cases (e.g. not enough string left for some terms to catch up). This is where we have to start approximating.

This solution: n-gram similarity

The best I could come up with so far works with phonemes. This particular version uses the last three phonemes (3-gram) of the target phrase to look up similar-sounding 3-grams. These are linked to places that terminate with exactly that 3-gram. Then with this subset I find the best match. Nice and simple.

So how does it perform? First, as you might expect at a glance, it is definitely going to be faster than an exact solution. I use all 39 phonemes from the ARPABET that are found in the CMU dict project, so there are 39^3 = 59319 3-grams. For each I pre-computed 40 of the most similar 3-grams to make the final sample size consistent and large enough.

More specifically, I started with a phoneme similarity matrix [1], then used a multi-dimensional scaling algorithm to embed this matrix 2D space, then concatenated the coordinates of each phoneme into 6D, and performed nearest neighbour on each term with a kd-tree.

At query time, this translates to a few exact index hits on tables with around 1000000 rows, for each of the approximately 10-100 phonemes in a phrase. Not shabby. The pre-computation was also pretty reasonable, taking less than an hour on my Macbook.

Well, I want better.

Okay, so we're only using a small chunk of strings for this first big narrowing step. What's the tradeoff? Looking at the histogram of number of phonemes:

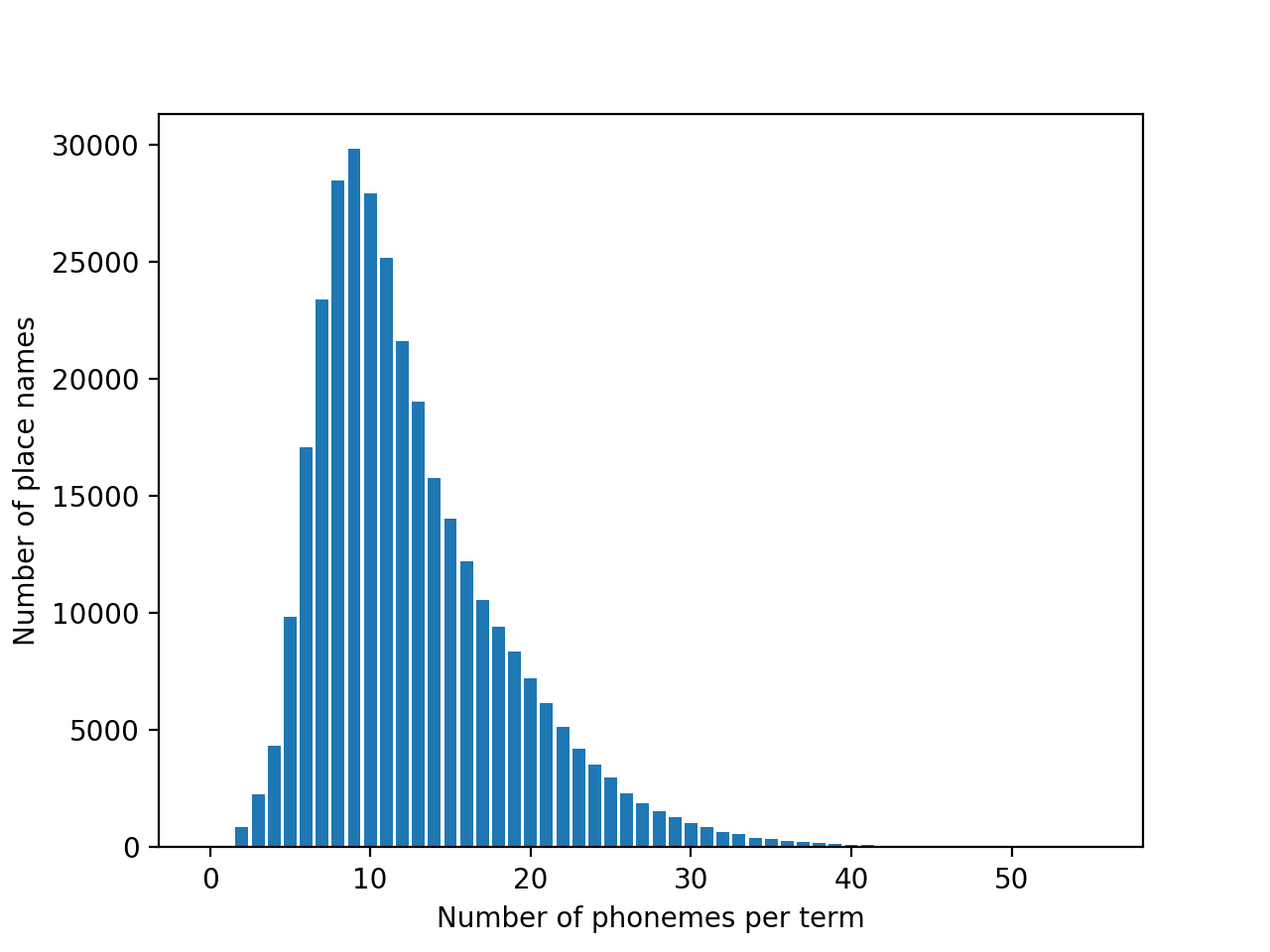
Histogram of phoneme counts with n phonemes

This is a little concerning. We're far below the mean, so most of the string will follow the unconditioned statistics of arbitrary string matching. Here is an estimate of that distribution:

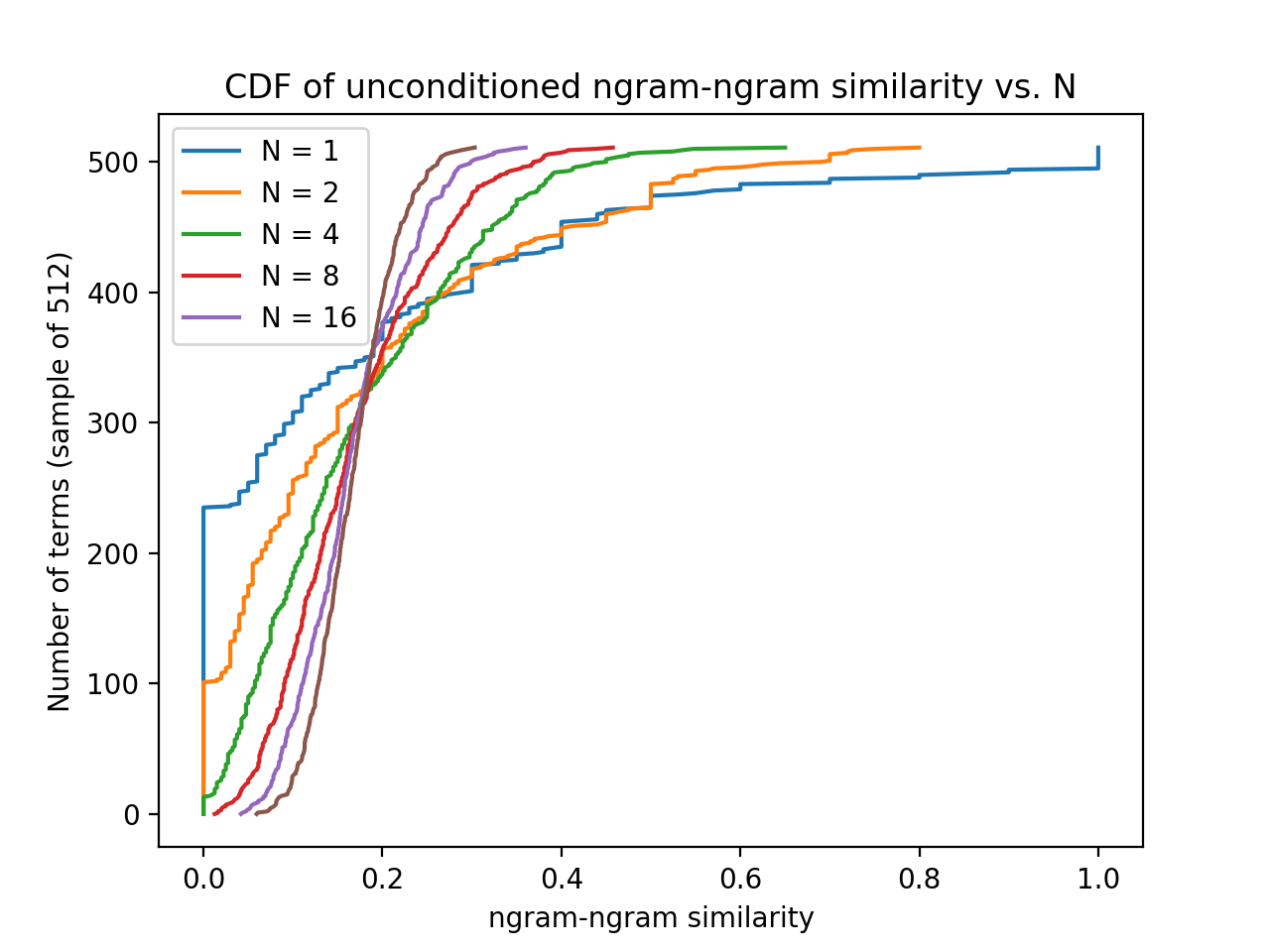
n-gram-n-gram similarity

This was generated by sampling elements from the similarity matrix and adding them, then sampling that result set and repeating, creating effective n-gram samples of length 2^k for k iterations.

We see the mean is around 0.2, and of course converges for more phonemes. Yikes. For reference, P (for "pit") and F (for "fit") have weight 0.26. Of course, we don't care about the mean directly: for each phoneme of the target, we are looking for the best match out of our sample. This turns into a maximum distribution with cdf $F_n = (F_1)^n$, and with the finite support $[0, 1]$, the distribution gets tighter and moves to the right with more samples.

How many samples? Let's look at the distribution of the number of place names per n-gram:

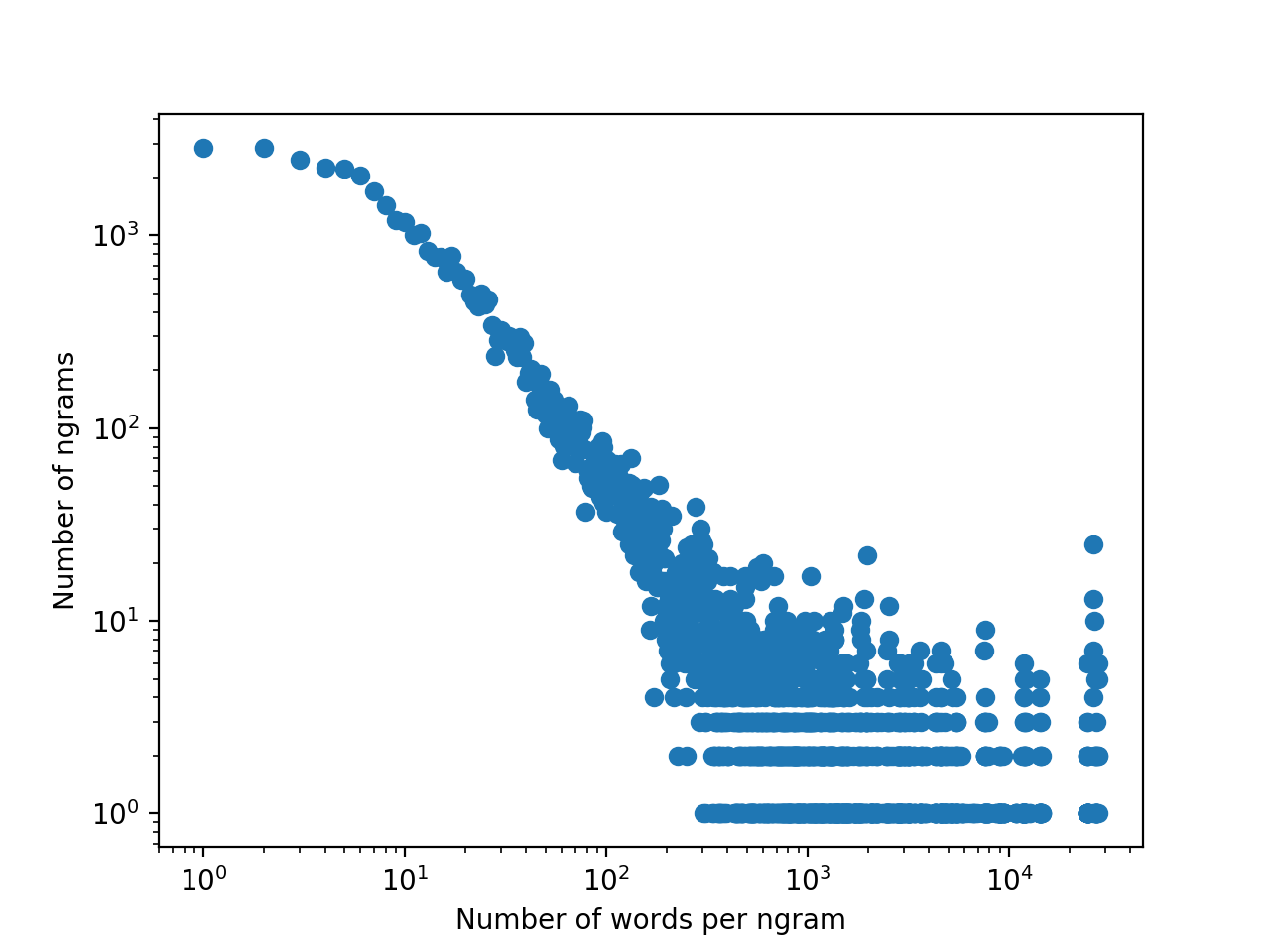
n-gram incidence

The mean is 266 names/n-gram (Zipf law parameter: 0.722). Given our sample 40 n-grams, this gives us around 10000 place names. I'm shaky on the maximum distribution of a sample of 10000 with finite support, so for now I can only offer the observation that sampling from the unconditioned 8-gram distribution matches pretty closely to the actual typical score from running the program, hovering around 0.5 for the matches beyond the first 3 exact ones.

So how can we improve this?

We can sample more points, although because 1 is an asymptote, the gains must be slowing down, while user impatience is superlinear in time probably... [definitely].
We can increase the $n$ of our n-gram, but anything above $n=4$ — where the number of permutations is $39^4 = 2.3\times 10^6$ — is unreasonable for complete coverage. Complete effective coverage is perhaps more reasonable: based on the Zipf law slope, we can cut twice the n-grams ($10^{1-0.722} = 1.89$) for every word we sacrifice.

Ultimately, we have a few fundamental tradeoffs. There's obviously search speed vs. result quality. Then there's the time, memory and indexing speed from pre-computation. The goal of pre-computation here is to add more context to the decision of reducing the sample space. N-grams for example guarantee a far-above-average score for the last n phonemes. My motivation to pursue n-grams is that they are very fast and improve scores directly and verifiably. In particular, I'd like to know if there are any strong correlations between small pieces of context and large strings, even if they are complex and language-dependent. The first to come to my mind didn't have enough power to make much of a difference, e.g. phoneme ↔ word length (to condition on the memoizing array $C$).

1/31/2020: I am running a 4-gram at the moment, will see how it does.

2/06/2020: How much farther is there to the top? To find out, I brute-forced a corpus of Reddit comments for the best possible solution with the place names I've got. I also compared this to the 3-gram's performance.

Alg	Avg. score/phoneme	N
3-gram	$0.80 \pm 0.05$	369
Brute-force	$0.88 \pm 0.03$	74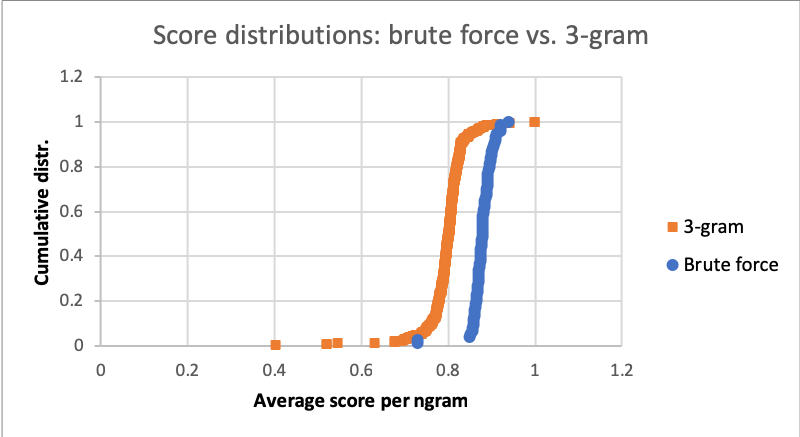

Comparison of brute-force solution to 3-gram

The fact that the 3-gram is actually pretty close to the exact solution hints at the fact that most matching terms don't tend to be much longer than n-grams long, and the sample size of 10000 additional places makes up for the rest. And all things considered, the exact solutions aren't all that great either. Some brute-forced solutions of random sample Reddit comments are in the below aside:

Score	Comment	Route
0.856	Yes, but less so each year. Doing a few a games a year with Grant has worked out well.	yesse → butler → sewee → choix → ayr → dew → inger → few → a → guemes → leer → wythe → grant → howes → weches → atwell
0.881	\$20? Look at Mr Moneybags.My vodka is \$9 for a half gallon. Tastes like liquid failure. Perfection.	luke → ott → mist → eure → vado → a → oz → farr → huff → gallant → ace → towle → ai → click → rudd → fay → loy → perfection
0.879	If your voter registration hasn't been purged. And you are able to take time off to vote. And your local voting location doesn't get closed down and you have to drive an hour or two to vote. And your voting machines register your votes correctly. And your state does paper backups. And your leaders don't destroy those paper backups when they get accused of interference. For sure.	f → yoe → eure → vote → wray → gist → shine → pheasant → bayne → paige → dunn → drew → r → abell → sutic → time → ough → chew → onda → orr → low → cull → ong → location → dow → zent → gate → kloze → nunn → harr → tudor → ai → vann → a → tatu → ink → shouns → register → vaughts → correct → lee → ona → norse → tate → dows → pape → back → upson → day → reeders → doane → trist → roy → vose → ops → wende → agar → tuck → hughs → dove → ain → tuff → ayr → anse → fourche
0.892	Even here they win with disinformation. Basically blasting conservative propaganda at them on every radio station, owning local TV broadcast station as well as the local pastor pushing conservative social views regardless of the downside of the rest of their platform	e → vin → hare → jay → wynne → wythe → days → ain → furrh → mission → basic → lee → bliss → timken → service → eva → rapp → a → gahn → dow → attu → m → ann → ever → wray → dee → ace → tesch → uno → ringe → low → cull → ti → v → broad → cost → stay → shine → azwell → oz → the row → culp → astor → push → ink → ansel → tiff → social → view → krug → ard → russ → eve → the downs → ida → via → rest → avoy → ayr → platform
0.880	Cowboy! When I got him he was about 6 months old and a surprise for my wife (girlfriend at the time). His name that we inherited him with was "Charchan's Rhinestone Cowboy." We shortened it to Cowboy. He is from a line of championship level pugs, is what I'm told. He's the best.	cowboy → way → nye → gate → home → hebe → oz → a → butman → ace → ohl → dunn → dow → surprise → fourmile → ai → furrh → earl → friend → atla → time → hayes → nims → ott → wea → ain → hare → tad → wythe → wise → rhyne → stone → short → urne → titu → hay → mull → love → champion → shipp → level → why → tow → lehi → xaya → best
0.851	You don't understand the argument that we shouldn't kill individuals because they have may have a tougher life than others? I'm not sure what I can say to change your mind if that's the case--we're much too far apart on morals to find common ground.	yewed → olton → dess → tandy → a → argo → mount → chatt → wea → shumont → killin → dove → edge → walls → bay → cosby → harr → may → havre → tuff → eure → life → zana → schurz → m → knott → shuree → tye → conn → satoo → chain → joy → orr → maine → dif → sattes → schumm → attu → farr → partain → murrell → fine → scammon → grande
0.857	I've been smoking for about 14 years, tried a few ciggies at a party and was a pack a day smoker after that. Over that time I've tried to quit 3 times using nicotine patches and each time I've been all good for about 6ish months and then something happens that drives me back to them.. One was a drunken mistake and the other two were stress related.I guess my question is what can I do to try and help not fall back into it next time when I try to quit?	ives → anse → meaux → king → farr → a → bow → toyei → wright → ryde → few → ott → partee → onda → oz → pack → dess → craft → eure → datto → verne → awe → time → tuck → whitt → imes → hughs → ong → nicut → ain → patch → lund → aitch → ai → aubin → all → goode → butman → theon → drenn → schumm → thick → hammons → sand → rives → may → back → tool → m → whon → maza → drumb → conn → stay → conde → louther → chew → west → rest → s → mike → wes → nisbet → dew → trian → day → elk → knott → foil → jewett → lex → way → knight → rye
0.879	I just watched this episode and loved the little spider!! Which is really saying something, because I do NOT like spiders at all. But that sequence was very well done. The whole show was terrific. I'm watching the North America episode now. I loved the part about the fire flys. Thanks for all your hard, wonderful work on this series.	ai → gest → wa'atch → trace → earp → a → saude → newlove → day → little → spider → way → chise → rylie → sage → isom → thick → bay → causey → dew → knott → lykes → pye → dows → ott → all → buttes → awe → tzeek → whon → swan → vair → e → weldon → the hall → scholle → oz → turk → fay → kime → ink → north → america → new → love → parr → tubb → duff → ayer → hanks → foy → rawl → york → ard → wonder → foules → eure → conn → jay → ceres
0.870	People are just horrible nothing new and those who seek to abuse their power flocked to those in control the church since it was harder to break into court from scratch. In modern times these assholes are spread out in politics, business, etc. in addition to abuse in the church.	pipaa → largent → horeb → aulne → utting → newald → vose → house → eek → tewa → muce → vair → powe → f → lock two → ain → kent → rolfe → a → church → sun city → oz → harder → tuber → aiken → tuck → ort → frame → scrutchins → odd → urne → time → zoe → zeus → hall → czar → spread → outing → pala → dix → bays → nye → sites → etter → dissen → blue → cinda
0.730	[removed]	rheem → ord
0.880	Well, it sat on a shelf for 10 years before they made it.	way → litz → ott → awe → nash → elf → orr → mears → bay → forebay → may → date
0.889	If it is in stock within X radius of you and you order before cutoff time, same day is possible. There's really nothing more to it. Since I live between 20 miles of 4 different Amazon warehouses I usually get same day or next day on a ton of purchases.	ai → faye → tees → anse → tok → wythe → ain → aix → wray → dee → a → dove → ewan → drew → ord → eure → bay → fork → ott → ough → time → simms → arizpe → asa → ballou → ayres → lena → thick → mort → pitts → sile → eve → between → miles → dif → arunde → amazon → ware → howe → zzyzx → hughs → waieli → gates → m → day → orr → hext → awe → nutt → love → purchase → oz
0.900	You gave a pretty good balanced answer to a difficult question. That's the dichotomy - it's difficult for most people to evaluate and accept a "balanced" response to an emotionally loaded subject.	yewed → ava → pray → ti → goode → bill → ernst → anse → eure → tewa → difficult → questa → neotsu → a → dye → cottam → e → oates → foremost → p → pearl → touhy → value → aten → dix → earp → tubb → allen → stry → spann → stuie → nimmo → schnell → load → aid → gest
0.867	This was actually the inspiration for the show “The Pretender”.	virsoix → zack → chew → a → leatha → ain → spur → ossian → ford → shaw → dupree → tent → eure
0.865	Lots of big events lost to history. I love learning things I didn't know, I didn't know!	lotts → eve → bay → bevent → sloss → chew → hester → e → ai → love → luning → kings → day → dunn → snow

Code

The code is hosted on GitHub. It includes the data massaging scripts, database schemas, and server/client code.

A shoutout to the projects that made this possible:

Data from the GeoNames gazeteer for US city names during development;
The North American OSM dataset for the current place name & coordinate data;
The CMU Pronuncing Dictionary and CMU's d2p-seq2seq to get pronunciations in terms of phonemes;
The work "Similarity and Frequency in Phonology" [1] for the consonant-consonant phoneme similarity measure (note: I personally sounded out and guessed the vowel phoneme similarity matrix);
scikit-learn's MDS and a kd tree to group n-grams (tuples of phonetic units);
The languages of the stack: PostgreSQL + Node + React, with Leaflet, OSM and OSRM.

[1] Frisch, S. (1996). Similarity and Frequency in Phonology. Unpublished doctoral dissertation, Northwestern University.

Use it: maps.lam.io
GitHub: acrylic-origami/reaction-maps