A basic acrobatic tail — Control and mechanics

I've been working on a 3-DOF arm for the last few months to use as a robotic tail. I was initially going to have it completed for Tomorrowland 2020 in mid-July, but when that was cancelled, the parts were already on the way here so I got it functional anyways and thought the design was worth sharing. It's no hyper-redundant manipulator (yet), but it's perfect for a cheap, strong and forgiving hand-build. See below for a preliminary demo:

I've distilled aspects of its control (here), mechanical build and electrical design that I think describe its distinctive features. I've kept these posts on the descriptive side in the hopes of explaining the construction and imparting some idea of the design space. They assume basic understanding of kinematics and 3D geometry, not too much seeing as I'm sure not an expert in either, either.

Outline

Broadly, the control for this actuator handles path-planning on XYZ inputs. It consists of:

Exact inverse kinematics;
An interpolator with bounded position excursion; and
A timing solver to respect torque-speed limits.

It strives to be computationally lightweight and visually plausible. It has the added constraint of needing to be soft on the actuators, which are all off-the-shelf RC hobby parts expecting to be strapped to a steering column, not half a kilo on a stick.

Computation

The control is implemented on a microcontroller, specifically an STM32F103 @48MHz with no FPU. The project including CubeMX setup files are available on GitHub, here. Broadly: the main loop processes position data from a hand controller and performs inverse kinematics via precomputed lookup table. I then interpolates actuator angles by solving safety constraints on torque and speed, and buffers the resulting spline to a 50Hz motion control loop that low-passes everything and PWMs it to the motors. A detailed description follows in the next section.

Actuators

The three actuators are:

A low-kV sensored brushless motor stepped down by a 51:1 planetary gearbox. The motor is 25.5-turn, 2-pole, 0.1Ω, 1520kV, rated at 70W with a expected stall torque of 2.5kgf·cm ungeared (130kgf·cm geared).
A "high-torque" standard digital servo by Hitec, rated to 16kgf·cm and 8.4V, with 150° travel.
A "high-torque" standard digital servo by ZOSKAY, rated to 20kgf·cm and 6.8V. (Really just one servo manufacturer on Amazon saturating the market)

For more details on the mechanical aspect of the kinematic chain, see the build post.

The actuators are oriented to produce pitch → yaw → pitch respectively, to balance style — it better be able to wag after all — with a decent coverage of the available volume.

Actuator design space discussion

20kgf servos typically address the niche of rock crawler steering systems: substantially higher torques targeting the R/C market thin out quickly. Robotic servos and their respective price points start to dominate torques around 30-40kgf—cm, as the motors become coreless or brushless. The actuators and the dimensioning for the design came together simultaneously, mostly driven by this constraint. I kept the driven weight within 1kg and the length within 1m to keep the worst-case load torque of joint 0 below 50kgf·cm, and ~20kgf·cm and ~10kgf·cm for joints 1 and 2 resp., assuming constant-ish linear density. It helped that most configurations brought the center of mass in and reduced the moment of inertia.

Joint 0 is a little hard to reproduce because it was improvised out of a [very insufficient] stepper gearmotor from which the planetary gearbox comes. Gutting the stepper for the input gear was unpleasant, and the 3D printed scaffold wasn't free, nor the most compact. I elaborate on this in my discussion of the mechanical build — in short, the most attractive alternatives would either be a dedicated gearbox, a specialty industrial 12V brushless gearmotor, or windshield wiper drivers.

Details

Input

This iteration of the hand controls consist of two 2-axis joysticks: a thumbstick on top, and a trigger-like input on the bottom of the controller. The feasible region is roughly hemispherical, so the thumbstick maps to azimuth and elevation, while the trigger maps to radius. These inputs are normalized and mapped directly to a lookup table for joint angles.

Inverse kinematics

Inverse kinematics were solved using IKFast with this OpenRAVE robot definition resulting in this C++ solver. At the top of this page is an interactive demo of the final inverse kinematics used in this design (at one fixed radius parameter).

The lookup table is 24KiB, with 16 entries per input dimension except azimuth with 8 entries due to the left-right symmetry of the arm. All positions in the tail's operating region (behind the wearer) end up having up to two solutions within the limits of the actuators (roughly ±π/2). These are disambiguated on the fly by choosing the solution with the least travel from the current orientations — the demo above only shows one of the solutions.

Live inverse kinematics didn't end up being worth it — the IKFast module compiled to more than 10kB, and since the inputs are so coarse anyways, that degree of precision in the IK is unnecessary.

^†Input remapping

The feasible region shown above in cartesian coordinates (looking at the right half, looking down from above) is roughly hemispherical. The colors shown In spherical coordinates, the feasible region takes on a quadrilateral shape in azimuth and radius (seen above mirrored about az=0°).

The controls were remapped by adjusting the radius range for each azimuthal angle to trace out the quadrilateral. For example, at the extremes of azimuth, the radius control collapses into one point. The demo from the previous section uses this remapping. The coverage and actuator angles are shown in the demo below. Image axes are X=azimuth, Y=elevation, and the slider steps through the radius ratio as rescaled at each azimuth.

Interplator

A good interpolation scheme can assure bounds on torque, speed and position excursion for the motors to avoid jank that could damage them. It is especially important for position-based control, where the setpoint from the controller moves much faster than the actuators can handle, so most of the time the actuators are moving along an interpolated spline.

The interpolation schemes I've been targeting to get things rolling interpolate each actuator separately, so they aren't sophisticated by any stretch. Contrasted to constrained path-planners of modern arms, I aimed for an interpolation lightweight scheme to run on the MCU and that could guarantee the derivatives of the endpoints. That's it.

My first instinct was to solve for a cubic in the angle domain with boundary conditions. I had used "cubic" splines like this in the past, like interpolating the spin on a 3D globe visual for a previous job, but I hadn't realized that such solutions were unbounded and performed very poorly at high boundary speeds.

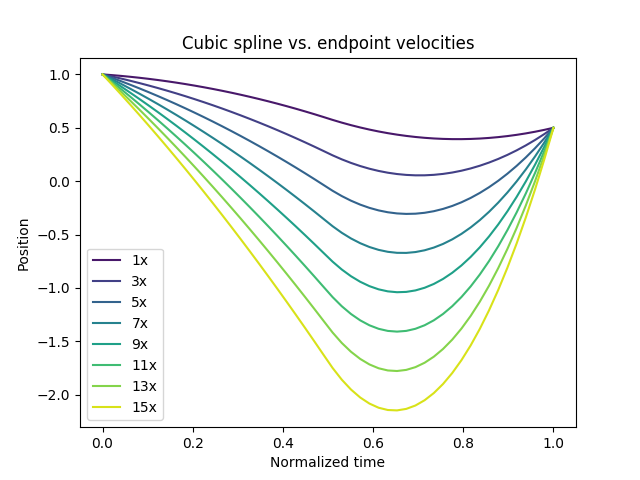
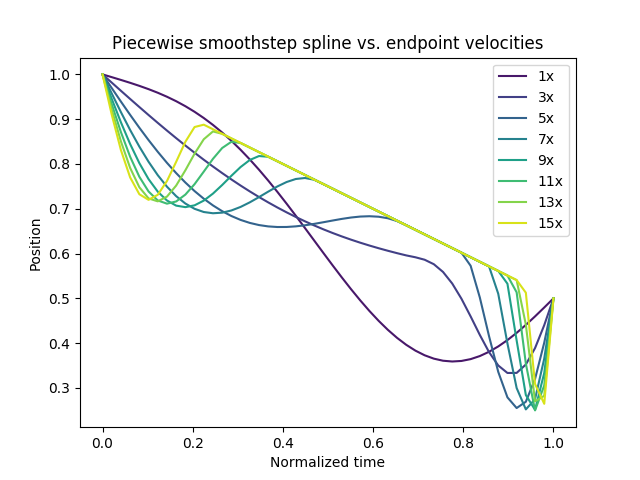
Next, I opted for a spline with guaranteed bounds instead, although at great expense to torque (bottom graph). The spline smoothsteps between slopes defined by the endpoint velocities to a slope between the endpoint positions.

(2020-07-21) The interpolation ~~is being migrated~~ has been migrated to one with 1D quadratic B-splines which can be bounded straightforwardly, and have gentle curvatures.

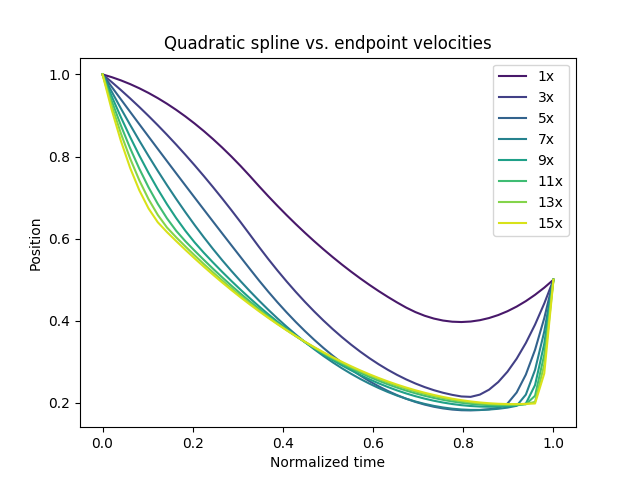
The spline has five control points: two at the endpoints, two that define the endpoint velocities, and one in the middle that I've fixed on a straight line between its neighbouring points. Nominally, the two inner control points are at T/6 and 5T/6 (a detail of the knot points being at 1/3 and 2/3 to give me a nicer torque in the middle). If either velocity is high enough, the bound $\Delta_0$ clips the control point, bounding the curve. In the example below, the second control point is bounded, so the first interval is shortened below T/6.

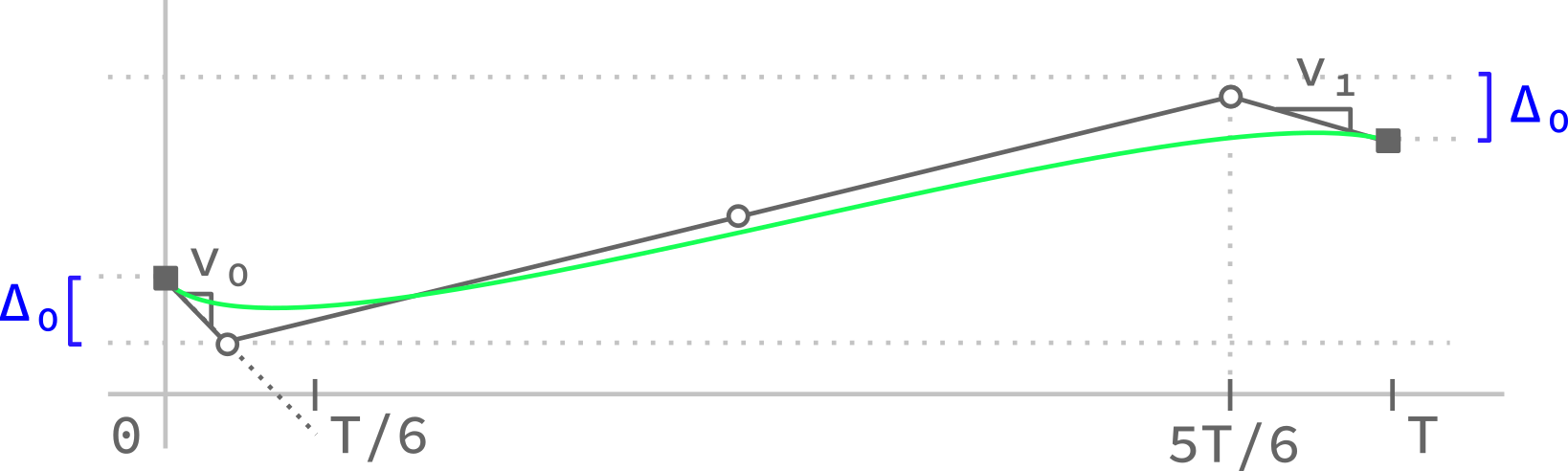
I've provided the Python quadratic spline implemntation I wrote to debug my quadratic spline here on GitHub. Included are an implementation of the raw quadratic spline as a function of knot points and control amplitudes, as well as a solver for these parameters based on endpoint positions and velocities.

Timing solver

The duration of travel ensures that the worst-case torques and speeds of the spline don't violate the limits of the motors. For the B-spline used in the current iteration, the travel time is progressively bounded by solving for the time that brings the worst-case torque and speed below the estimated torque-speed curve of the joint.

To simplify the calculation with symmetry, the motor safe operating area is modelled as axis-aligned ellipses with axes defined by stall torque and no-load speed. Worst-case torque and speed depend on the spline — for the current quadratic B-spline, there are only at most three torques and four critical points for velocity for each spline at each knot point, which is super computationally convenient.

We want to solve for the travel time $T^*$ where the worst case torque and speed of the spline lies on the safe operating boundary. Since torques and speeds almost always grow when travel times shrink, this should be the most aggressive trajectory that is still safe. For the elliptical boundary, this is just:

$$ \frac{\max_i\{\tau_i(T^*)^2\}}{\tau_{max}^2} + \frac{\max_j\{s_j(T^*)^2\}}{s_{max}^2} = 1 $$

The expressions $\tau_i(T)$ and $s_j(T)$ can be rather deceptive though. For the bounded quadratic B-spline, the variation of torque and speed with time is actually quite complicated due to the discontinuity at the excursion boundaries. This is important for the solver, which needs to estimate these derivaitives for step size. For example, here are some torque and speed derivatives with respect to the travel time $T$ after the control points hit the boundaries:

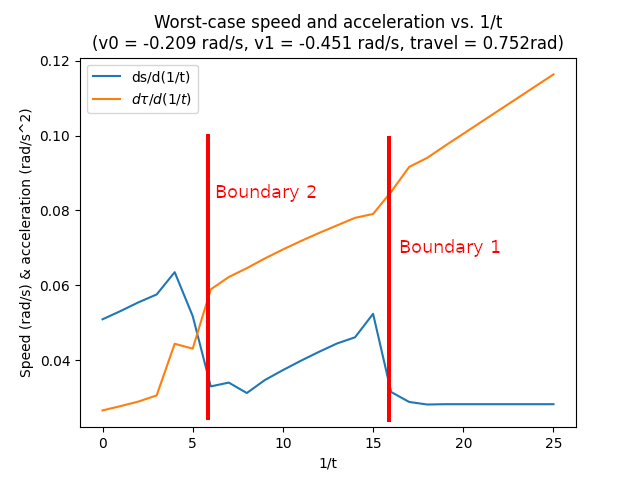
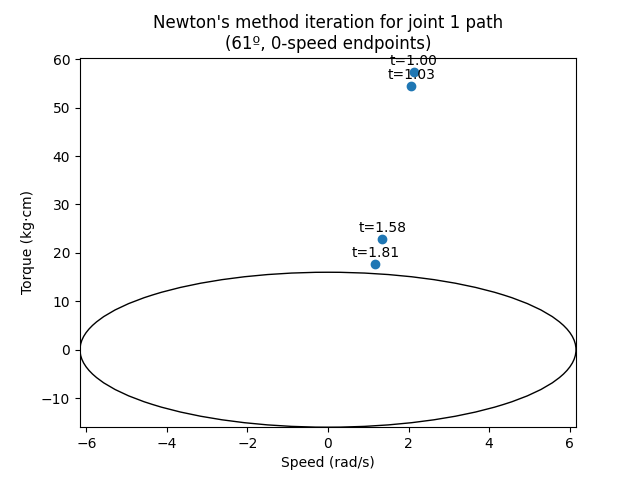
As a result, Newton's method solver is outfitted with a dead-simple 1D, 2-sample gradient descent rather than any fixed derivative expression. The plot below shows the solver finding the entrypoint of the torque-speed quadratic for a 61° path by joint 1. The initial point is chosen ~~at the SMAX speed~~ at 1.0s — a reasonable guess from experience. The timid first step is hard-coded to estimate the first derivative, then a couple of iterations later we get our result, which is 1.81s here.

GitHub: acrylic-origami/tail-3dof